심화기계학습: 차원축소
차원축소 분류: 변수선택과, 변수추출[선형, 비선형 기법)
변수선택 기법
Hughes Phenomenon: 훈련 데이터 수에 비해 차원이 증가할 수록 모델 성능이 점차 감소(데이터 밀도감소)
대표적인 차원 축소기법
PCA
목적: 데이터 차원 축소와 최대한의 분산 보존.
주성분: 공분산 행렬에서 가장 큰 고유값을 갖는 고유벡터의 방향으로 정의
(이 벡터들은 서로 직교하며 데이터들의 선형결합으로 표현)
왜 직교하는가?
중복 정보를 제거하고, 각 저성분이 독립적으로 데이터를 설명하기 위해
적용: 1) 데이터 행렬의 평균을 0으로 정규화 2) 공분산 행렬 계산 및 고유값, 고유벡터 계산 3) 고유값을 크기 순으로 정렬하여 상위 k개의 고유벡터 선택 4) X를 새로운 k 차원 공간으로 투영: Z=XW
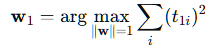
Multidimensional Scaling
목적: 객체 간의 유사성 또는 거리를 입력받아 저차원 공간에서 이를 최대한 보존하는 좌표 선택
적용: 저차원에서의 각 점 사이의 거리 d가 원래 거리 D와 최대한 비슷하도록 점들의 좌표 선택
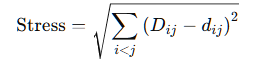
Isomap
목적: 비선형 차원축소기법, 유클리드거리를 사용하는 MDS와 달리 곡선경로 또한 표현 가능
적용
1) 각 데이터 포인트의 이웃을 결정(k-nn)
2) 이웃 그래프 구축(k개의 이웃과 연결되어 그래프 형성, 각 노드는 데이터 포인트를 나타냄)
3) 두 노드(포인트) 간의 최단 경로 계산(지오데식 거리 계산: 유클리드가 아닌 그래프에서 연결된 최단경로)
4) 저차원 공간으로 임베딩
변수추출 기법
Filter, Wrapper, Embedded
Filter: 모델 학습과 독립적으로 변수의 중요성을 평가하여 변수를 선택
상관관계나 통계적 테스트를 이용
Wrapper: 특정 모델을 사용하여 변수 선택
Stepwise regression(전진 선택법, 후진 소거법, 단계적 선택법)
mRMR (Minimum Redundancy Maximum Relevance) : 고차원 데이터에서 중요한 특성을 선택하는 필터 기반 변수 선택기법
적용
1) 변수와 타겟 변수 간의 상호 정보량을 계산하여 관련성이 높은 변수 평가
2) 선택된 변수들 간의 상호 정보량을 계산하여 중복성 감소(다중공선성 문제를 줄이는 방향)
3) 관련성을 최대화하면서 중복성을 최소화하는 변수를 순차적으로 선택
I(xi;y)는 상호정보량, I(xi;xj)는 변수 간의 상호정보량
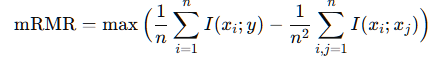
Embedded: 모델 학습 과정에서 변수 선택을 동시에 수행
Lasso 회귀, 의사결정트리 기반 특성 중요도 평가 등